Makale-Nikodemus saung Blog
1. Pengertian vektor

Pada garis berarah dari titik A ke titik B di R 3 mempunyai panjang tertentu dinyatakan sebagai vektor. Vektor dapat dinotasikan dengan :

Atau dapat juga dinyatakan sebagai :
Dimana adalah vektor satuan.
adalah vektor satuan.
2. Panjang Vektor
Jika titik A (x1,y1,z1) dan B (x2,y2,z2) maka vektor AB adalah :




3. Vektor Satuan
Vektor satuan adalah adalah vektor yang panjangnya satu satuan. Jika vektor maka vektor satuan dari a adalah:
maka vektor satuan dari a adalah:

4. Operasi Penjumlahan, Pengurangan dan Perkalian Vektor dangan Skalar
a. Penjumlahan atau pengurangan vektor
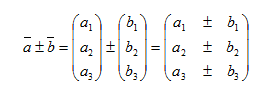
Contoh :
Diketahui vektor Nilai
Nilai 
Jawab :


b. Perkalian Skalar dengan vektor

5. Rumus Perbandingan, Perkalian Skalar Proyeksi dan Perkalian Silang Vektor
a. Perkalian Skalar

b. Cross Product
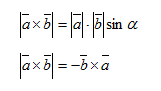







d. Rumus Pembagian
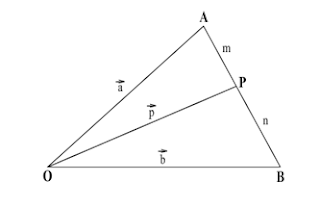

Contoh : Diketahui titik A (-4, 1, 3 ), B (6, -4, 3) dan C (4, 5, -1) Titik R membagi AB sehingga 2AR = 3RB, vektor yang mewakili adalah :
adalah :
Jawab :


Read more »
1. Pengertian vektor

Pada garis berarah dari titik A ke titik B di R 3 mempunyai panjang tertentu dinyatakan sebagai vektor. Vektor dapat dinotasikan dengan :

Atau dapat juga dinyatakan sebagai :

Dimana
 adalah vektor satuan.
adalah vektor satuan.2. Panjang Vektor
Jika titik A (x1,y1,z1) dan B (x2,y2,z2) maka vektor AB adalah :




3. Vektor Satuan
Vektor satuan adalah adalah vektor yang panjangnya satu satuan. Jika vektor
 maka vektor satuan dari a adalah:
maka vektor satuan dari a adalah:
4. Operasi Penjumlahan, Pengurangan dan Perkalian Vektor dangan Skalar
a. Penjumlahan atau pengurangan vektor
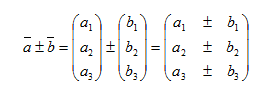
Contoh :
Diketahui vektor
 Nilai
Nilai 
Jawab :


b. Perkalian Skalar dengan vektor

5. Rumus Perbandingan, Perkalian Skalar Proyeksi dan Perkalian Silang Vektor
a. Perkalian Skalar

b. Cross Product
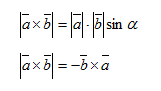







d. Rumus Pembagian


Contoh : Diketahui titik A (-4, 1, 3 ), B (6, -4, 3) dan C (4, 5, -1) Titik R membagi AB sehingga 2AR = 3RB, vektor yang mewakili
 adalah :
adalah :Jawab :



 Blog RSS Feed
Blog RSS Feed Via E-mail
Via E-mail Twitter
Twitter Facebook
Facebook